.rst .pdf

open issue suggest edit

Contents

Linear and Ridge Regressions Computation

Batch Processing

Linear and ridge regressions in the batch processing mode follow the general workflow described in Regression Usage Model.

Training

For a description of the input and output, refer to Regression Usage Model.

The following table lists parameters of linear and ridge regressions at the training stage. Some of these parameters or their values are specific to a linear or ridge regression algorithm.

Linear RegressionRidge Regression

Training Parameters for Linear Regression (Batch Processing)

Parameter	Default Value	Description
algorithmFPType	float	The floating-point type that the algorithm uses for intermediate computations. Can be float or double.
method	defaultDense	Available methods for linear regression training: defaultDense - the normal equations method qrDense - the method based on QR decomposition
interceptFlag	true	A flag that indicates a need to compute \(\beta_{0j}\).

Prediction

For a description of the input and output, refer to Regression Usage Model.

At the prediction stage, linear and ridge regressions have the following parameters:

Prediction Parameters for Linear and Ridge Regression (Batch Processing)

Parameter	Default Value	Description
algorithmFPType	float	The floating-point type that the algorithm uses for intermediate computations. Can be float or double.
method	defaultDense	Default performance-oriented computation method, the only method supported by the regression based prediction.

Online Processing

You can use linear and ridge regression in the online processing mode only at the training stage.

This computation mode assumes that the data arrives in blocks \(i = 1, 2, 3, \ldots \text{nblocks}\).

Training

Linear and ridge regression training in the online processing mode follows the general workflow described in Regression Usage Model.

Linear and ridge regression training in the online processing mode accepts the input described below. Pass the Input ID as a parameter to the methods that provide input for your algorithm. For more details, see Algorithms.

Training Input for Linear and Ridge Regression (Online Processing)

Input ID	Input
data	Pointer to the \(n_i \times p\) numeric table that represents the current, \(i\)-th, data block.
dependentVariables	Pointer to the \(n_i \times k\) numeric table with responses associated with the current, \(i\)-th, data block.

Note

Both input tables can be an object of any class derived from NumericTable.

The following table lists parameters of linear and ridge regressions at the training stage in the online processing mode.

Linear RegressionRidge Regression

Training Parameters for Linear Regression (Online Processing)

Parameter	Default Value	Description
algorithmFPType	float	The floating-point type that the algorithm uses for intermediate computations. Can be float or double.
method	defaultDense	Available methods for linear regression training: defaultDense - the normal equations method qrDense - the method based on QR decomposition
interceptFlag	true	A flag that indicates a need to compute \(\beta_{0_j}\).

For a description of the output, refer to Regression Usage Model.

Distributed Processing

You can use linear and ridge regression in the distributed processing mode only at the training stage.

This computation mode assumes that the data set is split in nblocks blocks across computation nodes.

Training

Use the two-step computation schema for linear and ridge regression training in the distributed processing mode, as illustrated below:

• Step 1 - on Local Nodes

• Step 2 - on Master Node

Algorithm parameters

The following table lists parameters of linear and ridge regressions at the training stage in the distributed processing mode.

Linear RegressionRidge Regression

Training Parameters for Linear Regression (Distributed Processing)

Parameter	Default Value	Description
computeStep	Not applicable	The parameter required to initialize the algorithm. Can be: step1Local - the first step, performed on local nodes step2Master - the second step, performed on a master node
algorithmFPType	float	The floating-point type that the algorithm uses for intermediate computations. Can be float or double.
method	defaultDense	Available methods for linear regression training: defaultDense - the normal equations method qrDense - the method based on QR decomposition
interceptFlag	true	A flag that indicates a need to compute \(\beta_{0_j}\).

Step 1 - on Local Nodes

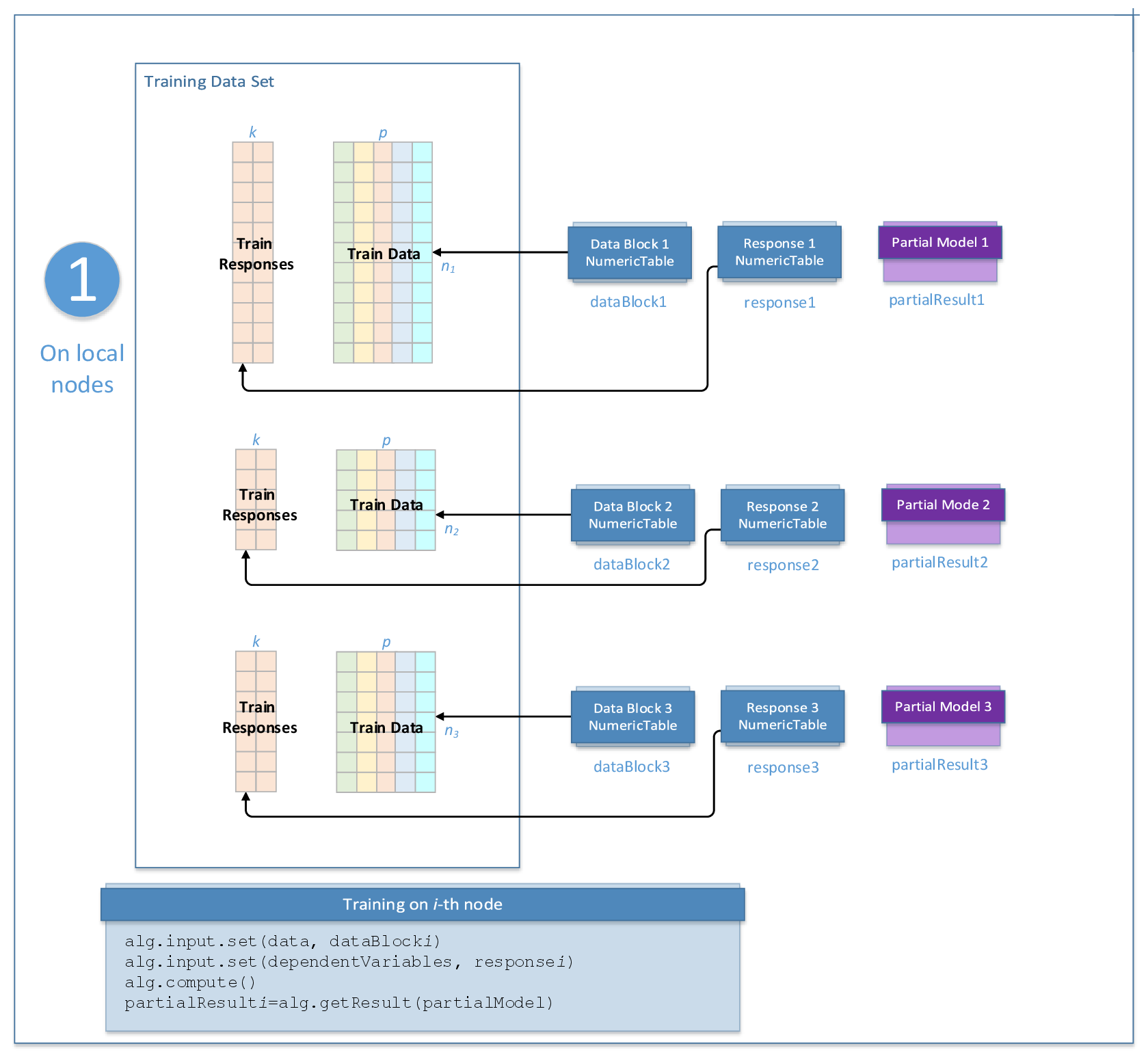
Linear and Ridge Regression Training: Distributed Processing, Step 1 - on Local Nodes

In this step, linear and ridge regression training accepts the input described below. Pass the Input ID as a parameter to the methods that provide input for your algorithm. For more details, see Algorithms.

Training Input for Linear and Ridge Regression (Distributed Processing, Step 1)

Input ID	Input
data	Pointer to the \(n_i \times p\) numeric table that represents the \(i\)-th data block on the local node.
dependentVariables	Pointer to the \(n_i \times k\) numeric table with responses associated with the \(i\)-th data block.

Note

Both input tables can be an object of any class derived from NumericTable.

In this step, linear and ridge regression training calculates the result described below. Pass the Result ID as a parameter to the methods that access the results of your algorithm. For more details, see Algorithms.

Training Output for Linear and Ridge Regression (Distributed Processing, Step 1)

Result ID	Result
partialModel	Pointer to the partial linear regression model that corresponds to the \(i\)-th data block. The result can only be an object of the Model class.

Step 2 - on Master Node

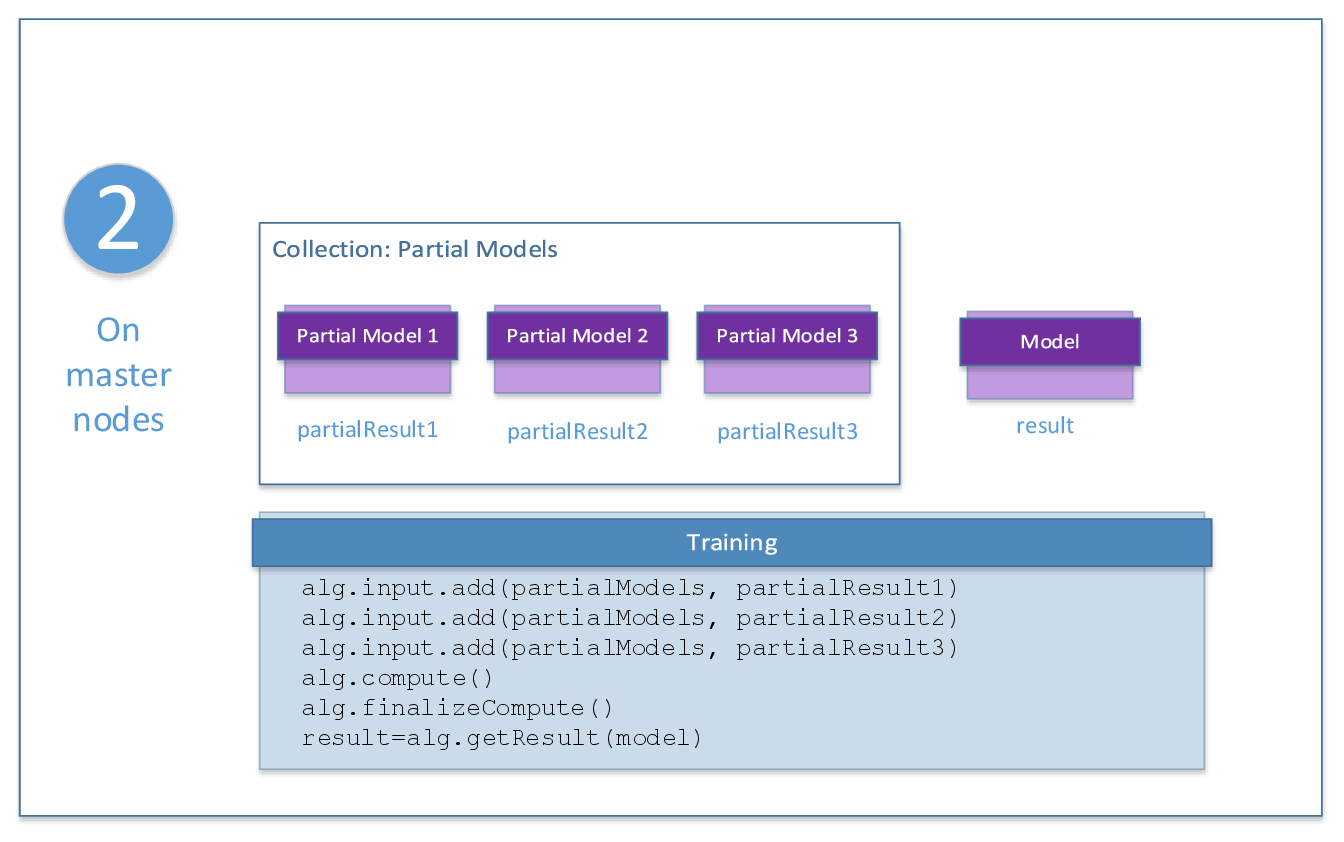
Linear and Ridge Regression Training: Distributed Processing, Step 2 - on Master Node

In this step, linear and ridge regression training accepts the input described below. Pass the Input ID as a parameter to the methods that provide input for your algorithm. For more details, see Algorithms.

Training Input for Linear and Ridge Regression (Distributed Processing, Step 2)

Input ID	Input
partialModels	A collection of partial models computed on local nodes in Step 1. The collection contains objects of the Model class.

In this step, linear and ridge regression training calculates the result described below. Pass the Result ID as a parameter to the methods that access the results of your algorithm. For more details, see Algorithms.

Training Output for Linear and Ridge Regression (Distributed Processing, Step 2)

Result ID	Result
model	Pointer to the linear or ridge regression model being trained. The result can only be an object of the Model class.

Examples

C++ (CPU)Java*Python* with DPC++ supportPython*

Batch Processing:

• lin_reg_norm_eq_dense_batch.cpp

• lin_reg_qr_dense_batch.cpp

• ridge_reg_norm_eq_dense_batch.cpp

Online Processing:

• lin_reg_norm_eq_dense_online.cpp

• lin_reg_qr_dense_online.cpp

• ridge_reg_norm_eq_dense_online.cpp

Distributed Processing:

• lin_reg_norm_eq_dense_distr.cpp

• lin_reg_qr_dense_distr.cpp

• ridge_reg_norm_eq_dense_distr.cpp

previous

Ridge Regression

next

LASSO and Elastic Net Regressions