Subgraph Isomorphism¶
Subgraph Isomorphism algorithm receives a target graph \(G\) and a pattern graph \(H\) as input and searches the target graph for subgraphs that are isomorphic to the pattern graph. The algorithm returns the mappings of the pattern graph vertices onto the target graph vertices.
Operation |
Computational methods |
Programming Interface |
||
Mathematical formulation¶
Subgraphs definition¶
A graph \(H = (V'; E')\) is called a subgraph of graph \(G = (V; E)\) if \(V' \subseteq V; E' \subseteq E\) and \(V'\) contains all the endpoints of all the edges in \(E'\) [Gross2014].
Further we denote the induced subgraph on the vertex set as induced subgraph, the induced subgraph on the edge set as non-induced subgraph.
Computing¶
Given two graphs \(G\) and \(H\), the problem is to determine whether graph \(G\) contains a subgraph isomorphic to graph \(H\) and find the exact mapping of subgraph \(H\) in graph \(G\).
\(G\) is called target graph, \(H\) is called pattern graph.
Mapping is a bijection or one-to-one correspondence between vertices of \(H\) and a subgraph of graph \(G\). Two vertices are adjacent if there is an existing edge between them, and non-adjacent otherwise. Induced subgraph isomorphism preserves both adjacency and non-adjacency relationships between vertices, while non-induced subgraph isomorphism preserves only adjacency relationship.
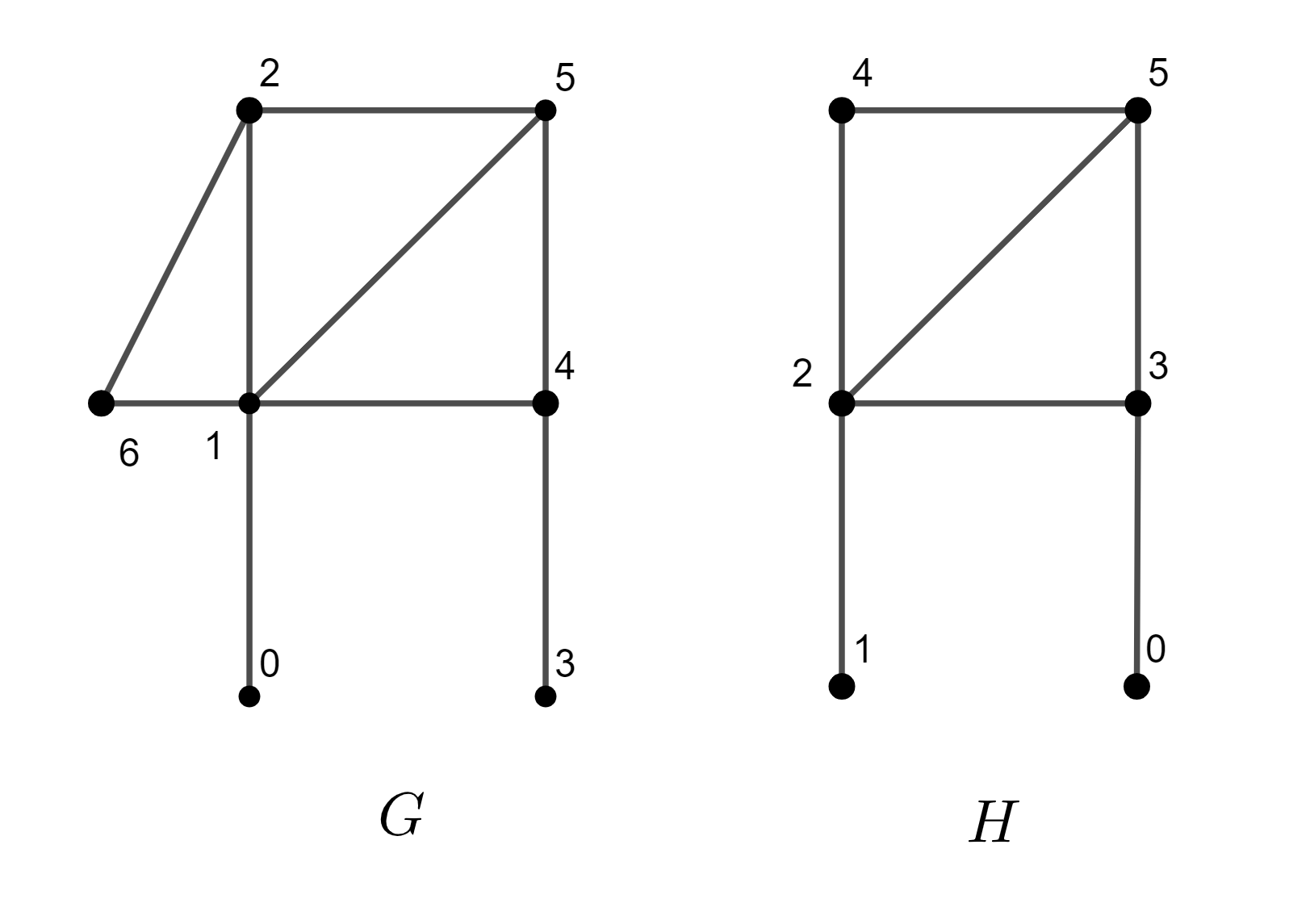
Example
For the example above, the mappings for subgraph \(H\) in graph \(G\) are:
Induced: [3, 0, 1, 4, 2, 5]
Non-induced: [3, 0, 1, 4, 2, 5] and [3, 6, 1, 4, 2, 5]
The notation [3, 0, 1, 4, 2, 5] means that:
pattern vertex with id 0 is mapped on vertex in target graph with id 3
pattern vertex with id 1 is mapped on vertex in target graph with id 0
pattern vertex with id 2 is mapped on vertex in target graph with id 1
pattern vertex with id 3 is mapped on vertex in target graph with id 4
pattern vertex with id 4 is mapped on vertex in target graph with id 2
pattern vertex with id 5 is mapped on vertex in target graph with id 5
Computation method: fast¶
The method defines VF3-light algorithms with Global State Stack parallelization method and supports induced and non-induced cases.
For more details, see [Carletti2021].
Programming Interface¶
Refer to API Reference: Subgraph Isomorphism.
Examples¶
Batch Processing: